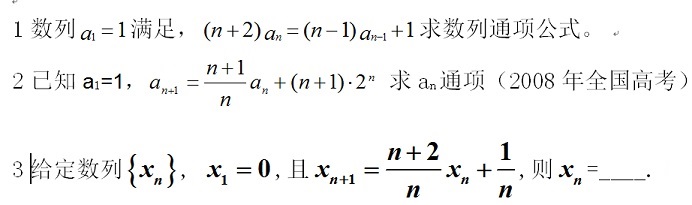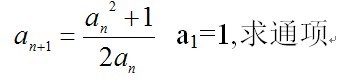我也读过高中,经历过重点高中的磨砺,所以我与学生一样有着亲身的体会:中国的是一个“考试”型的教育国家。中国的高中生只能以考试为目标。高考命题的专家们,就是整天在搞透脑子去出题,目的就是怎么用“考题”把“差”生筛选掉!
我们只能适者生存,以考试为己任。然而高考出题,历年都是多样化,很多“考点”并非仅仅依附在教材基础上,多数都是在基础上进行“升华”“演变”的。在教材上必然都不能直接找到。而以教材上的基础知识为垫脚台的“演变知识”和“升华知识”,只能靠教师去研究考题,去抓考试的规律,去研究,去总结。所以要讲得出深刻的东西,是需要“创”出来的。
考点不停地在演变升华着,而国内传统课堂在“正课”很少会跟上步伐。包括国家一级重点高中在内(如学军,二中,附中等权威重高)的多数传统在职老师在正课中,大多都是去讲述教材上的最底层基础知识,或是在基础知识上略作扩展的牵连知识。但这种“略有扩展”远远达不到中国考试命题的高度,远远还不能覆盖试题规律上。 这样在正课中讲不到的,但遇到考题又不得不去面对。这种考试知识的演化多样性,与课堂上知识传授的单一性,这一矛盾,在传统重点高中的解决方法就是:“做题。” 碰到题目把你难住了,用这道题牵扯出来的东西给你讲,那些教材上的基础知识怎么去运用,去演变,去升华。
我并不是说搞海题不好,搞题海有它的好处,比如增强学生的运算和解题的熟练程度。所以做题是必要的或者说是必须的
,尤其是到了高三,所有方法和思维全会了后,一定要通过题海,才会对曾学过的方法知识达到熟练应用的目的。但
如果在一开始知识空白的初级阶段就搞题海?有没有“真正去弥补”先前我说的正课中的漏洞?
(更有甚者是很多传统课上,仅仅就只是给学生告知解题过程,很少能把题目中蕴含的知识思想本质用一般性的方式给学生"讲出来"。)用做题方式去“补充”正课中没有的空白,住住会导致以下情形:
|
A学生从题目中往往只是学习了这道题或同类题的解法,而题目中蕴含着的一般性的方法思维,学生是学不到的。这一条,可以简言之就是:买椟还珠!学生看到解法后,自认为“懂”了。这仅仅只是得到了一个表面
解法,题目中蕴含着的统一规律与技法学生根本就没有学到。他的头脑中“能
随时自发性地调用的知识结构”依然是空白。最后学生往往只能常握了这道题,
(临时掌握,过段时间说不准他又忘记了)根本就不会把这题中所学到的补充的知识进行推广应用于其它问题中。
B正课中学到的东西不需载体,是“独立地”,“全方位性的”去学习,这样的学习必然是全面性的,
更多细节性的。之后,这些知识在学生头脑中是建立起了一种框架,一种概念结构,之后是能做到“自发性”地去运用
这种概念结构去思考,快速调用之前的方法。这样先这些知识全讲透着讲完全再去练题,才能达到教与学的最佳效果。
反之,只在习题中去学习某个知识,学生就会受到习题环境下的限制,对知识很多细节上都是“模糊”的理解,不必说,是不会把它运用到其它环境中的。
C我印像中,用题去补充正课中没有讲过的知识,往往都只是在这道题中培养其中的某种“主观感觉”,培养盲目性的“做题惯性”,往往导致学生失去了数学原始的“推理”的本性,而“主观感觉”“主观惯性”代替了逻辑推理,占据成为学生心中的主导地位。失去逻辑推理的本性,是正规大考中最致命的弱点。因为正规大考中的题不会出现你之前做过的题,而全部是新命的题。
D在题目中去学习正课中没有的知识时,师与生双方都将“做题”视为了戏的“主角”,而知识被列为“配角”。这种解法怎么来的,为什么要这样做,这是什么原理?解题老师对于这些多都是不讲的(或者讲不全面透彻。因为讲解一个知识难点,教学中是需要备案,备课,条目梳理,达到讲清前后每个“细节”,最后还得强化训练巩固。也只有正课才有这个环境,仅凭在做习题的环境下,是没有这个条件的。自然学生当时懂了也只是临时懂了而已。)最后反正是教你做了,以后记住这样做就行了。同时,学生也感觉是这样做,会做了,却没考虑下次再碰到它的变形,但是应用同一知识点的题目时,还能不能自发的通过推理做出来? |
所以,这样堆积题海经验,学生学不到知识的本质层次上,最后治标不治本。 任何一场正规的大型考试,试题全是“新”题,你以前的主观惯性与经验,在大考中是用不上的。我依稀还记得当年在一中高三的时候:高考前夕学校的3次模拟考,我们班部分人次次都是140+以上了,在寝室中讨论都高考完后要报北航天还是报北理工,结果高考成绩一出,都是70-80分。。。连二本都难,最后免强上了个河北经贸。(当然那个同学大学毕业后考上了公务员。最后居然是最牛的人。)
这是我当年读高中最深刻的体会,也是目前我带的学生中了一直存在的普通问题。正是当年我在学生的时候就发现了以上原因,所以我当年就想当老师。长大了如愿当了老师,就要专门对考点知识点进行梳理,找出里面的统一规律和通用的思想方法,再把这些方法,全都要在“正课中”就去给学生讲清楚,明确其原理是什么,什么环境下去调用它们……
(这些也是现今传统教学中,20名老师中有19名老师都不会讲的东西。也就是说你找20名老师,运气好可能会碰到里面有1个能讲到全面周到的,运气不好的话个个全是只会给你解题。这20名老师,包括国家一级重点高中内的在职老师,也包括40-50岁之上的教了20多年的所谓“资深”老师。)
从某种角度上说,我也在给学生培养“某种惯性”,但区别在于,由于我对上述中的问题非常敏感,所以我绝不走以前自己曾走过的路线,我教学生,一定要直接“覆盖到考点”上。你可以看到学校课堂上讲函数就用那本高一教材,函数内容在整本书,只有3章:5-6节的样子,传统课堂一个学期5个月中有1个月在讲正课,4个月都在做题讲题。而我上述截图目录就是我的教学计划,函数的内容目录有20多节。这20多节多出来的东西,全部来源于平时的小考,大考,以及历年的高考中,统一知识规律和精华。相信业内人,一看目录就清晰明了:节节都直扎在考点上!这些经过长期教学钻研梳理出的,全都是你在国内任何地方也见不到的“精品思维”。一学期5个月时间,我需要2个多月讲基础知识,再2个月做题强化。那还剩1个月,可以回家睡觉打电子游戏去了!
(这里切不可误会我绝没有否定搞题海,有的时候做题搞题海也是必要的,尤其是运算能力差的学生,必须多计算多做题。但我们应该是先学通方法,像很多重高的在职老师,大多都是方法还没讲呢,就直接就上难题了。这样学生最后题就算会解了又有什么用?)
用中国俗语解释就是:“磨刀不误砍柴功。”
教学精彩之处及与传统老师的内容区别
(不懂数学的这里请跳过,直接看最下面)
毛主席说:别光喊政治口号,枪杆子下才能出政权。教学说到底还是要看课堂内容。我要是讲不出东西来,不可能有前面那些对话截图,更不敢会在这里这么大口气。
高中数学最难的三大难点就是:函数,数列,解析几何,针对文科生的话,立体几何也是头疼。以下所举内容即为这几处的难点教学实例。这些是能让杭州国家一级重点高中内的多数平平的在职老师见到后怛然失色的东西。懂数学的一看就懂,不懂的看也白看
。
实例1:高一函数章节授课内容
对应必修一,几乎90%之上都是教材上没有的,多数课堂老师也不会专讲的(只是做到题时讲那道题的解法),反而在考试中接2连3地出现的!并且也是很多高中生读到高三还
有空白的东西!

实例2:为什么那么多学生对函数的奇偶性总是学得糊涂?
大多数课堂不讲奇偶性的基础知识台阶,螺丝杆不打纹就要拧上去,这叫硬套!
以下是网上一个“教研论坛”中各个教师们的讨论内容截图

图片尺寸问题文字不太清晰,我把贴子内容复制到在下面:
"
每个地方标准不同,记得我在山东的时候。有个奇函数下周,大致是已知一个含有参数a的奇函数。可以根据奇函数性质(把参数a)求出来,做选择题常用的手机是f(0)=0.但是解答题就不严密了。当时我们的一致意见是解答题必须用定义再去论证。结果,07年重庆高考题的标准答案就是用f(0)=0求出来的!
今年重庆这边高考评分标准规定:只要是教材中出现的习题结论,或者著名的定理,都可以作为推理的依据。……"
云烟的观点:
多数传统老师们之所以认为“不严密”,“最后还需用定义论证”,究其原因,是很多老师一直就没搞清奇偶性的定义式:f(-x)=-f(x)其本质------恒等式。甚至很多课堂对“恒等式”,这是什么东东,压根就不存在!高考的标准答案,实际上正是严密的推理。如果后面再加上论证反而是“画蛇添足”
连很多在职老师自己解题,都完全把“恒等式”这一“根基”抛到了九霄云外,怎么能去教懂学生?
还有从奇偶性上演变出的更高一级的难点:函数若有对称轴x=a则会满足f(2a-x)=f(x),这东西教材上没有,老师在主课上也就不讲了,等碰到题目时才会和学生说。但关键是---往往在试卷中常考难点,恰好都是教材上和平时课堂的空白之处。你都见过了还考有什么意思?就考你在教材上都没见过的!!!
实例3:解析几何 高二高三最综合的内容
截图是其中的一节:切线与切点弦

切线一节,在我近两年中,部分前8所和几乎全部的16所学校中,90%以上的同学压根就不知道切线代换是什么东西。只有各别前三所的重高高三生说,有印像,学校老师用过这种方法,记得在讲哪道题的时候用过。当然前三所的同学还有的同学会拿出的课堂笔记,但笔记上面记的,只是一个圆心在原点的正圆的代换式。(学生并不理解)
我这里要说的是:我所讲的“代换法”,是适用于全部二次曲线(椭圆,双曲,抛物,正圆,打勾,反比,分式),而不是像前三所那些所谓资深传统老师那样,只是在做到那道题时才讲,而且他们只讲正圆的。包括学军的高三资深教师所出版的资料书《圆椎曲线.....》里面所提到的,也只有针对正圆,所以我怀疑:连那些在职老师自身就根本不知道:代换方法还能用于椎圆,双曲等全部曲线!
(由于学校课堂很多老师只讲正圆的代换式,并且大多数不是主动讲,而是在遇到题目时发现不得不采用这一方法求解而被动式地去提出来,这样的后果会导致给同学们一种错觉:这种方法好像只能用在正圆上,不具备一般性,以致大多数同学在看到老师用这一方法解题时,会怀疑它的实用价值覆盖度,也就会无视掉,对之不理采。而即便各别同学会记在笔记里,记下他也不会用。)
----------------------------
实例4:解析几何
2013年5月,杭二中新高三生,女生,基础较好,头脑聪明,数学题海阅历广泛,在高一高二的2年中已经堆题无数。
但是看到这两题,做到后面就搞不灵清,
最后做不出来。

之后该生学习了这堂课:

在课上学生听到中途就“发现新大陆”了,心情开始高涨兴奋,一边听一边就把题给解出来了,等我刚讲完原理和方法,然后说开始做做这几道题时,她说:“老师我做出来了!......” 。然后她大发感慨:“哇,以前就是做题做很多,都理解不透,原来是这种“原理”,以前根本都不知道呀!”
这堂《动态中的恒定性质》也属于云烟个人钻研了20多年高考及各模考试题后,苦心整理而提炼出的精华。)
实例5:数列的中高端难点,也是大众盲区(别小看这高一的内容,这是包括重高拨尖生学到高三,学3年都糊涂的东西)
2013年2月,春节期间正是补课高峰期,然而学生中的一位大神(杭二中高一实验班的拨尖生)临时请假不来上课。
随后家长电话里告知:“....她们学校老师放假期间家里开课了,平时机会都很少,名额有限,报名晚了的话就挤不进去了,所以我提前给她报个名,这段时间想让她先去二中家里上几堂,就10次左右
,上完了再接着来你这里继续上......”
我在电话中也表示了理解。(本人绝不会小心眼的啦。毕竟是国家一级重点高中的权威在职老师,寒假在家开课,对学生来说机会当然难得。)
大约有个10多天后学生上完那边课程,来我这里时,她把在那边听课的笔记都拿了出来,问了很多她一直没搞懂的东西,我一看她笔记,正是
数列的一阶线性递推式。
下面重点来了,学生的笔记上记的,是一阶线性递推的常考,大约是6,7种题型模板如下:(后悔当时没有拍照拍下来)
1常系数类型:an+1=A an+B, 处理的方法是......
2指数项类型的:an+1=A an+qn 处理的方法是.....
3关于n的一次类型:an+1=A an+(kn+b) 处理方法是.....
4因系数为1时的类型:an+1=an+..... 的处理方法是.....
5 ......6......7...... |
学生学了这么多种形式,依然还是有很多题还是不会做,比如下面的这3个例子:
(已经学到这的高一和所有高二高三生,知道我是要表达什么!不懂数学的这里就随意看看吧!)
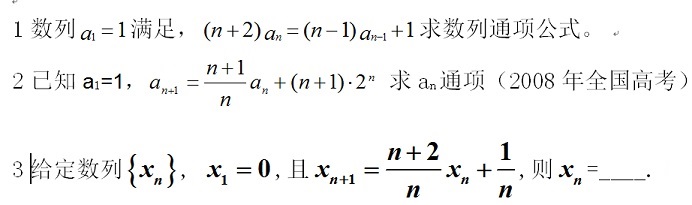
看不懂的,我这里说明一下:为什么不会做?因为前面那6-7种形式,在类型上并没有覆盖到这种考题!学生只是学了6-7个“点”,考题可以命题命出“几十个甚至超百个点”,你只学过6,7个点当然覆盖不到。
然后,我给学生看了我在这块知识的讲法,同时还告诉学生:“你这一堆东西,10多天的课程,我这就1堂课,而且比你的更彻底”如下:
|

该节讲述了一阶线性递推的统一处理方法为......,其统一的原理........
考试拿满分保障的花瓶摆法为........
|
云烟课堂对这个知识的讲法,不仅囊括了上面的6-7个点,实际是把这一递推领域的题目全部100%覆盖。并且在方法上统一成了一个东西,所以只需一堂课搞定,不需要4-5堂或7-8堂,就2个小时,学生全通,什么叫全通,就是学会后,高一到高三所有的题全拿下!(这1堂课学生所能学及到的深度,以及彻底性,远远超出她在外面在职老师家中学了10多天的效果!)
这位学生当年看完瞬间被毁了三观,马上就全明白了一切,同时呼吸变得紧促,有点激动,当时学生眼珠子就已经发了绿光.......,
我发现这个情况后,为了让家长从鼓里清醒,就给家长发了信息如下:
(还有这一节之前的基础数列求和,云烟讲法更精彩!只有2大方法,就拿下高一到高三全部求和问题。
|
我经常给同学举这个比喻:这个题型你学了10种方法,可是这10种方法的每种具有一般性吗?你外出探险,你随身带一了一身的武器,放大镜对付咬你的蚂蚁,弓箭用来捕猎,战刀对付恶狗,手枪对付老虎,大猎枪对付狮子……总之你带了一身!你会发现,手枪打不死蚂蚁,而放大镜照不死恶狗,弓箭杀不死狮子,又会发现突然某一天,天上飞来一个UFO和外星人对你人身将产生威胁时,此时你的所有的这一身的武器全部显得那么无助。那么,如果你在出发前只带一样武器:核
反应激光手枪,还会有那种无助吗?见蚂蚁一枪,见老虎一枪,见猛兽一枪,见外星人还是这一枪,所有对你的威胁全是这一枪解决,数学上,这就叫方法的一般性!!!一般性的就是:通吃!有些方法不具备一般性,你越学,你的水平就越低,而有些方法就具备一般性,这才是我们真正要学的方法!!(在下一页中所提出的另一个例子:高一函数值域,说的也是这个问题) |
实例6:数列,深度拨高性难点(这段内容不到一定火候我不会轻易讲,一旦开讲就要让学生彻底学透)
2013年6月,我在学军高一学生卷子上看到这道题: (难题)
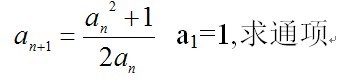
可以说这种数列递推型,是连10年经验的老师看了都心慌的题,有些老师就是像百度查找解法那样讲给学生听:左右两边同时加1。
(学生听完后首先产生的疑惑:谁能想到在左右两边加个1呀?这明摆的太无厘头了!)是的,这一方法就是只能用在这一道题上,原题换几个数字,
原方法就行不通了,所以学了也白学,学生们照样还是不会做。
比如:我再拿出一道同类题型:

上面这些题,是左右两边加个数还能行吗?我在这里敢说:以上这些同类变式,多数学校的老师不用说讲,他们连解都解不出来,而少数像前3所重高的一些竞赛教练自己的确能解出,但是学生听完也学不会。因为老师解出这题,他们自己都不知道里面的规律在哪里,而是凭借自己多年的经验和“数感”去“凑”出来!
这种凑,连老师自己都讲不出里面的方向性和规律性。
而我所讲的方法,是我苦心钻研这一专题而总结出的统一规律,是真的比那些学校的在职老师,多下了几倍的教研与心血,才探索出来的东西。我讲的是“根部的”,“通用的,” 是能让优高的基础平平的学生上完这堂课后,
就能把上面图片中的同类任意变式的题全部拿下的通用方法!基础较差的学生照样也能学会!当然有些计算能力太差的学生学会了,最后却由于马虎而算不对,很是气人!。 这部分是数列中算是深度难点了
,前面的基础还不到一定火候时我不会开这堂课。
(有一位比较清高的目中无人的杭高女生家长--可能就是在职老师装成家长来探风也说不定,看到我上面这些东西,问了我一个很专业的问题:“这种题型连前三所的学生都学得费力,你那普通优高学生他们能学得会???”
我回答的是:“你家学生学不会,是因为他学不到“根基上”的规律!”)
实例7:立体几何是个奇怪的章节,圈内生说立体几何比初中题还简单,圈外生说立体几何好难!
|
可能是云烟个人天生就有立体空间感。在高中学生时代,立体几何章节就是云烟老师个人科目内所学的最强的章节,也是云烟个人最喜欢玩的章节。当然当了老师后,更是达到炉火纯青级别。
立体几何的援课内容,完美到连“形式”都一模一样,每一个考点都是教给学生两把武林神器(倚天&屠龙)再后备一把地外文明(星战激光)。没啥好讲的。


|
有一些心态不好的喜欢好事的人看见后会说:"你这算什么?
我也有很多好评,但是我不像你这么张扬,你教得好你就这么往自己脸上贴金?你不懂得作为老师本身就应该谦虚与做人低调品行吗?....."
这是某年,杭州19楼论坛的家教版区,某位同行老师看到云烟发的贴子后
,大肆批驳的回复,原话引用。我只能说
:教学就是教学,展示自我教学的质量,无可厚非。何必扯一些与教学无关的道德绑架?
在这种混乱的教育培训环境,只要我保持着一种自己的一种纯洁,是以事实作说话的根基,给外界以真相,从不会像一些不良的机构那样杜撰虚编,就对得起良心了!
个人自荐:真正能讲出本质方法的老师 可遇不可求
|
老师不要看经验,老师的经验可以是10年20年,你认为学生,也能像老师那样学
个10年学20年吗?老师什么题都会解,学生不会解,这并不是因为学生笨老师聪明,而是咱们没把学生和老师放在一个公平的天平上去衡量。
对于老师来说,一个高中数学他学了十几年(而且他只学这一科,不学其它科),学生只有三年的时间
,同时还要顾及其它科,如果他也想像老师那样堆经验,从经验里去体会感悟数学,再慢慢去接近或达到老师十几年的水平,这对学生来说是: 太不
公平了吧?
解题厉害的老师往往有两种,一种是靠堆积经验,一种是靠教研和原理上的建立与梳理。前者,自己解题解出来,但是自己都说不出“怎么想到的?”,所以说一些老师就算教上20年,什么难题竞赛题都会解,他的教学质量也可能是平平无奇。后者,往往都是在心血研究中总结出的统一的万能的原理
规律,其解题也是用一种“统一性”的方针指导在逻辑上很“合理地”“自然地”找出解法,他所传授的也正是这种统一的原理方针。
我是一名高中数学老师。我的教学时间5年不算长,
(云烟老师于2009年开始教高中数学,此文写于2013-2014年。)但是在数学教学上,自信在教学质
量能做到国内一流。最关键的,我是上述文字中两种老师中所述的:后一种!
虽然我的教学经历也在年年上涨,但是我从来不用,甚至反感以“教学
经验有多少多少年”来给自己包装。
另外声明一下,我不是在职老师.....
很多传统老师,就算“资历”很深,一上课就给学生讲题练题,上节课练了哪些题,这节课再做哪些题。而却很少会去专门讲解题用到的“通用”的知识和思想,有自主性学习能力的
,聪明的学生,往往不会认可。“授人渔”,说的轻松,实上有多少老师真正做到了? (“深资”这词我到今也不知道是什么意思,是不是教上20年就是“深资”?)
不要错过真正能讲出本质方法的老师。就算你去重高里面一个一个去翻也一样,很多老师,尤其
思维上较传统的,保守的,包括权威重高在职,和普通高中在职,多是沿袭老一套:讲题,练题,讲题,练题。为什么这样解,这是什么思维?不讲!只给你讲解题。所以,就拿抽像函数来说,学生从高一就碰到这样的题型,一直练到高三!
学了快3年,还是一片迷雾的彼彼皆是。很多老师都把年龄当成自豪的资本,我看来毫无关系。
我是讲方法的老师,抽像函数我不需三年,我自创教法只要2小时学生就通!要搞清抽像函数,必须先讲清楚什么是“恒等式”(…此物国内90%之上的课堂上都讲不出来)。然后再去讲解函数三大特性:奇偶性,对称性,周期性。(...对称性也是很多课上见不到的)
最后原理搞清,六脉打通,站在这些地基上再去讲解抽像函数是什么。学生自然就大悟了,紧接着再针对这一问题阐述抽像函数处理方法:“抽像变换”(个人独创,国内极有可能只有我一人。是能让学生甚至是那些所谓重高资深的同行老师拖着下巴去听的内容,也是我在函数章节最自豪的教研部分之一)学生听完,就能从本质上会做了。会做了还不够,保底我还要把具体“方法流程”这些细节也讲出来,讲授我自创的最直观的“二步循环法”(我比喻为“老子生儿子,儿子老子联手打鬼子”学生印像深刻)这样步步为营!
我要保证:学生以后再碰到这样的抽像函数,不管高一的还是高三的,“全部”拿下。我们的效率:2小时>3年!
上面提到的这些东西,杭州前8所和前3所90%的课堂上是否会开设专题课专门讲解?是讲得到还是讲不到?你应该去问问你家学生,一定要去问。不怕你问,就怕你不问!!一定要去问,一定要问!
这里不排除学校也有个别有着自己一套的老师,他们善于钻研,能讲出统一的原理。这样的老师都是非常可贵的,我想每个学校也存在着这样出色的老师。然而毕竟真去给学生钻研教学的好老师数量不多,100名
中你能碰上1名,算是你中了彩了,你的幸运。但往往你没有那么幸运。包括国家一级重点高中等权威重高,每个老师头上都有“杭二中在职”“唐山一中在职”等这类头衔,但多少是照本宣科,又有多少能真正讲到本质层次上?值得你怀疑。
我 不敢说自己是人才,但是在高中数学这一领域,在中国
的高考数学考试钻研总结和梳理上,我有自信敢说处于国内尖端领先之列。只是,你一定要先排除与教学根本不相关的
因素,尤其是
排除:在没有听我真正讲课之前,只是事先电话中听到我的声音,或看一我的聊天工具的头像等,就在主观上
产生各种干扰或偏见。(这些也体现出了您的行为的浮躁和草率。)
你知道吗?曾经我没有建立这种全面性的介绍时,做为一个外貌
太显年轻的老师
,还有谈吐的声音清晰但不够“沧桑”,这些外貌特征,在一个以大众思维模式思考的家长心目中,不是一个专业级老师应该有的“特征”。所以,当陌生家长在电话另一头问:你教学是怎么教的,教得好吗?我回答:我教学很系统化,方法上比在职老师讲的更具有一般性,我比杭州前三所重高的很多在职老师教得都好。电话那头会马上传出一阵笑声:是吗?格格格格,我们不需要教得那么好哦,不好意思哦!还有的家长
由于在电话中听到我谈话的声音的“音色”不够沧桑,就直接翻脸说:你是哪个学校的老师?你教过高中数学吗?但是一旦他们看到我收集这些图片截图,之前讥笑的家长,就再也笑不出来了,之前翻脸的家长,就很快地变得慈祥了。所有偏见的人都换了一种语气,换了一种态度,多了一点人与人之间的平等和对人的尊重。
正是因为我在早期,碰到太多这样的家长及这种可笑或可悲的交流模式,即便事实摆在那,我也根本就没有机会去解释和展示。所以有时我的话中难免带着一些情绪,很多是由于这个社会的主观,浮躁而造就了我在这方面的“反弹”。最终,我不得不在这个主页置放了这么多家长对话截图,先是证明展示我的教学能力和教学效果,其次也是这个社会的浮躁与人心的浮躁所“逼”出来的无奈!
还有家长曾说:“云烟老师你很牛啊
!我回答:是!不过我牛的地方是教学,不是为人。教学上,我不只牛,是极端非常很牛。只是在我顶着玷污中华民族“传统
的”美德的罪名说这种高处不胜寒的形容词时,我起码还有教学能力这样一个站脚点支撑着
!
其实之前我也不知道我很牛,只是后来越来越多的人说我很牛,无论是真心还是调侃,总之最后我也学会了说自己牛,虽然我并不喜欢用牛不牛来形容一种教学,而是这一个浮躁的社会,与浮躁的人心,把我逼到了这一程度。最后我发现:自己不仅教学上要教得更好,还得要找到各种办法,能向外人证明和展示我教的好这个事实,这才是牛!
对了,还把我逼得学会了建立网站,和制作网页,折腾服务器。虽然本人知道这网页制作确实不怎么滴。(不过咱只是为了展现料子)
而本有的那一份纯洁,就让它藏在心底吧。
|